Feature Selection in Linear Regression Analysis
One of the most important problems in regression analysis is the selection of predictors in the model. The resoson behind this is we are often not satisfied with the least squares estimates.
First of all the least squares estimates have low bias and large variance. Since we sacrifice bias to reduce the variance to improve the overall prediction accuracy, this cause a problem. Also, with a large number of predictors, interpretation becomes problematic. In order to see the whole, we are willing to sacrifice some little details.
In this post, I will describe a number of feature selection methods with linear regression. Later, I will write a post about shrinkage and hybrid approaches, and other dimension-reduction strategies. However, n this post I will try to explain how the four variable selection methods(All Possible Best Subsets, Forward-Stepwise, and Backward — Stepwise) work and how they are implemented in R.
All Possible Best Subsets
In this method, first univariate models, then bivariate models, then trivariate models (until the total number of predictors is reached). The best model is decided by considering some criteria. If there are k candidate variables, 2^k possible models are obtained.
At this point, “some criteria” needs to be explained. The best model with $k$ predictors is chosen with the tradeoff between bias and variance, along with the more subjective desire for parsimony. There are number of criteria you can use: R², Adjusted R², C_p, PRESS_p , AIC(Akaike Information Criteria), and BIC(Bayesian Information Criteria). I have aldready write a post explaining R² and Adjusted R² . You can read that post in here.
Cp
Cp value measures the difference between the prediction performance and the complexity of the model. Cp is calculated using the following formula:
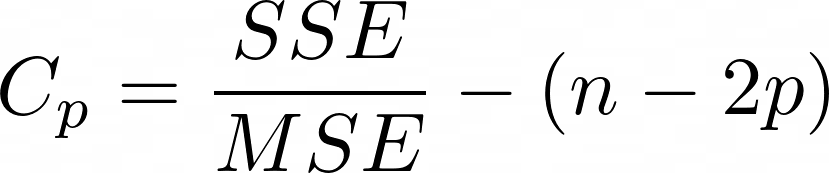
where,
-
SSE represents the sum of squared errors of a model.
-
MSE represents the mean squared error of a model without p independent variables (including only the constant term).
-
n represents the number of observations.
-
p represents the number of independent variables (predictors) in the model.
It is desirable that the Cp value is close to the number of parameters in the relevant model.
If $C_p = p$, there is no bias.
If $C_p > p$, there is bias.
If $C_p < p$, a sampling error has been made.
PRESSp (Prediction Sum of Squares)
PRESSp value represents the sum of the squares of the prediction errors for each observation value of a model. This value is a measure that should be lower. A lower PRESSp value indicates that the model has better prediction performance.
PRESSp value is calculated using the following formula:
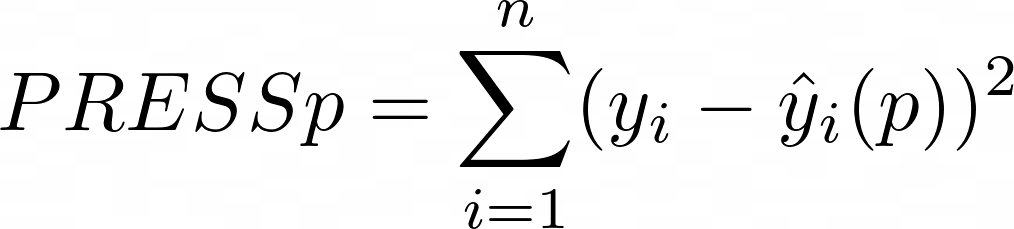
where,
-
y_i represents the observation value,
-
\hat{y}_i(p) represents the predicted value of observation i using a model with p predictors,
-
n represents the total number of observations.
NOTE: According to the Hastie, Tibshirani, and Friedman(see references), this is the best metric to choose how many predictors will be used in the model.
Akaike Information Criteria(AIC)
AIC value represents the difference between a term measuring the fit of the model and a term measuring the complexity of the model. The lower AIC value, the better balance the model is considered to have in terms of both fit and complexity.
AIC value is calculated using the following formula:
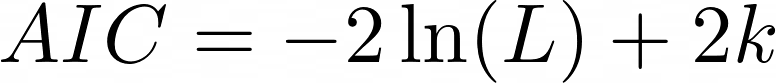
where,
-
ln(L) is the natural logarithm of the likelihood density function of the model,
-
k represents the number of free parameters in the model.
Bayesian Information Criteria(BIC)
BIC, like AIC, measures model fit and complexity, but BIC is a criterion by which more complex models are penalized more. BIC supports the principle of parsimony and encourages simpler models.
BIC value is calculated using the following formula:
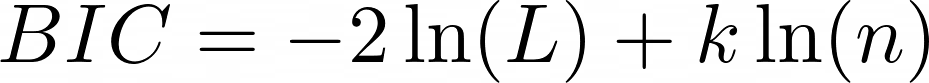
where:
-
ln(L) is the natural logarithm of the likelihood density function of the model,
-
k represents the number of free parameters in the model,
-
n represents the number of observations.
In R, `olsrr` package have ols_step_all_possible function for best subset selection. The following code chunk explain how it is used.
library(olsrr)
all.steps <- ols_step_all_possible(model)
view(all.steps)
When you run this code, you will get a dataframe like the following:

Also, it is possible to draw plot of the criterias with model index number. The following code and output show it:
plot(all.steps)

Forward-Stepwise Selection
If predictor number is more that 40 best-subset selection becomes infeasible. Forward-stepwise selection is both computationally and statistically preferable as it works by adding variables to the model at each step. It uses the F test as a criterion for adding variables. The added predictor is not removed from the model. If the F value is greater than $F_{in}$, the variable is added to the model. It can be said that it is more questionable than the best-subset method since it is not checked whether the variable added in the previous step will be removed in the next step.
In R,`olsrr` package also have ols_step_forward_p function for forward-stepwise selection. The following code chunk explain how it is used:
forward <- ols_step_forward_p(model)
forward
Selection Summary
------------------------------------------------------------------------------
Variable Adj.
Step Entered R-Square R-Square C(p) AIC RMSE
------------------------------------------------------------------------------
1 Price 0.1980 0.1960 289.6568 1882.4564 2.5323
2 CompPrice 0.3578 0.3546 154.9971 1795.5428 2.2688
3 Advertising 0.4571 0.4530 72.1640 1730.4006 2.0888
4 Age 0.5236 0.5188 17.2478 1680.0742 1.9590
5 Income 0.5403 0.5345 5.0052 1667.8346 1.9269
------------------------------------------------------------------------------
Its output only shows the selected model with predictors. Thus, you can use the selected model and continue to your regression analysis.
Backward-Stepwise Selection
Backward-stepwise selection works in a very similar way to Forward-stepwise selection. The difference is that it starts by taking all predictors into the model. If the F value is less than $F_{out}$, the variable is removed from the model. This process continues until there are no more variables to be removed from the model. Just like Forward-stepwise variable selection, it is not possible to re-introduce a dropped variable into the model.
In R, `olsrr` package also have ols_step_backward_p function for forward-stepwise selection. The following code chunk explain how it is used.
backward <- ols_step_backward_p(model)
backward
Elimination Summary
---------------------------------------------------------------------------
Variable Adj.
Step Removed R-Square R-Square C(p) AIC RMSE
---------------------------------------------------------------------------
1 Population 0.5403 0.5345 5.0052 1667.8346 1.9269
---------------------------------------------------------------------------
NOTE:
Taking all variables at the same time may cause Multicollinearity, which is one of the assumptions of linear regression. I will analyze the assumptions in more detail in the next article.
Just like always:
“In case I don’t see ya, good afternoon, good evening, and good night!”
Reference and Further Reading
Hastie, Trevor, Robert Tibshirani, and Jerome Friedman. The Elements of Statistical Learning: Data Mining, Inference, and Prediction. Second Edition, pages(57–60) Springer, 2009.